CALCOLO COMBINATORIO
PERMUTAZIONI - DISPOSIZIONI - COMBINAZIONI
Termonologia
di base
Nel
calcolo combinatorio si usa una operazione chiamata
"fattoriale"
e si indica con !
Il
fattoriale e' il prodotto a scalare di una quantita' pari a 1 FATTORIALE
= ! = n! = n * (n-1) * (n-2) ..... * 3 * 2 * 1 es:
4! = 4 * 3 * 2 *1
a
partire da una quantita' (o numero) iniziale
|
|
Si indicano con [ n ]e sono le quantita'a disposizione per formare dei raggruppamenti | |
|
gruppo |
Si indica con
[ k ]
e' la quantita di "oggetti", "presi" tra gli n elementi, che un gruppo puo' contenere k=n ogni gruppo contiene una quantita' k di "oggetti" identica agli elementi n k < n ogni gruppo contiene k oggetti i quali sono un sottoinsieme degli n elementi, i quali pero' possono o non possono ripetersi k > n significa che ogni gruppo e' formato da k "oggetti" che, essendo come quantita' superiore a n, devono inevitabilmente ripetersi per arrivare alla quantita' k" |
|
|
ordine successione |
Si intende il modo/ordine come si
susseguono gli oggetti (n) o parte di (n)in un gruppo es: dati gli oggetti 1,2,3 abbiamo due modi in cui e' possibile contare i casi in cui si possono disporre per formare un gruppo: 1) Gli oggetti (tutti o una parte) formano sequenze diverse: esempio 321 e 123 o 312 sono 3 oggetti disposti in 3 gruppi ma con diverso ordine. Sono cioe' 3 casi/gruppi/insiemi distinti, perche' pur contenendo gli stessi oggetti l'ordine in cui si succedono e' diverso: Queste possibilita' si verificano nelle PERMUTAZIONI e nelle DISPOSIZIONI 2) Gli stessi oggetti anche in sequenza diversa costituiscono un unico caso 321 e 123 o 312 sono in questo caso, identici ovvero formano un unico gruppo/insieme Viceversa 324 e 235 sono 2 gruppi/insiemi distinti perche' contengono almeno un elemento diverso tra loro Questo e' il caso delle COMBINAZIONI | |
|
|
Sia nelle PERMUTAZIONI nelle DISPOSIZIONI e COMBINAZIONI Lo stesso oggetto puo' ripetersi in un gruppo, ma in due diverse modalita'. 1) Gli oggetti possono ripetersi perche' sono gia' dati in partenza come ripetuti, cioe' sono oggetti uguali. es: AABB sono 4 oggetti da 2 si ripetono identici 2) Gli stessi oggetti possono pero' ripetersi, in questo caso moltiplicarsi,un numero determinato di volte, nei ragguppamenti che si formeranno, es: 01 sono n=2 oggetti che possono pero' formare in un gruppo k=8 la combinazione 10010010 |
Nelle PERMUTAZIONI , DISPOSIZIONI e COMBINAZIONI
i valori di [ k ] e [ n ] sono utilizzati
in precise formule per calcolare le diverse possibilita'.
Nelle applicazioni, la difficolta' a volte consiste nel capire
quale valore assegnare a [ k ] e quale a [ n ]
ANTICIPIAMO UNA SINTESI
| PERMUTAZIONI |
||
Tutti gli insiemi k devono contenere n elementi elementi: |
||
| essere presenti nell'insieme k n=4 [ A B C D] |
|
|
| |
||
| ma la somma a+b+c deve essere |
| |
| |
|
|
|
DISPOSIZIONI |
||
Le sequenze degli n elementi devono essere TUTTE diverse |
||
| |
||
l'insieme k puo' essere < n o >n |
|
|
|
COMBINAZIONI |
||
Un insieme deve differire dall'altro per almeno un elemento La sequenza non e' importante: ABC e BCA non sono 2 combinazioni ma una. |
||
| |
||
| |
||
LE PERMUTAZIONI SONO LA RICOMBINAZIONE DI [ n ] ELEMENTI
sono caratterizzate da:1) l'insieme [k] deve SEMPRE contenere TUTTI gli [n] elementi
[ k = n ] 2) Le sequenze (l'ordine o sucessione)di tutti gli [n] elementi devono essere tutte diverse SI hanno 4 casi di PERMUTAZIONI
1) PERMUTAZIONI SEMPLICI
Nessun elemento di n si ripete (es: pecora)
***
2) PERMUTAZIONI CON UN UNICO ELEMENTO CHE SI RIPETE ANCHE PIU' VOLTE
Caso di permutazione di ripetizione ma caratterizzata da un solo elemento di [n]che e' ripetuto nella sequenza data
( es: apina) ***
3) PIU' ELEMENTI CHE SI RIPETONO PIU' VOLTE
Caso di permutazione di ripetizione ma caratterizzata da piu' di un elemento
di [n]che si ripete nella sequenza data
( es: fanfaluca) *** ***
4) ELEMENTI NON RIPETUTI DISPOSTI IN CIRCOLO
Nessun elemento di[n] si ripete ma la sequenza e' disposta come in un cerchio
(es: 1 2 3 4 5 6 7 8 9 10 11 12)
PERMUTAZIONI SEMPLICI
numero di anagrammi di una parola con lettere tutte diverse La formula per calcolare questo numero di permutazioni e': P(n) = n! ES: anagramma di GIORNALE = 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
PERMUTAZIONI CON RIPETIZIONE
1 SOLO ELEMENTO RIPETUTO PIU' VOLTE
numero
di raggruppamenti di[ n ] elementi
con uno solo che e' presente (ripetuto) piu' volte
perche' contiene un elemento (a) che l'unico che e ripetuto
ma non pappa (2 elementi ripetuti: [p] [a])
Gli insiemi che si possono formare non devono essere identici cioe' non devono contenere sequenze uguali
ma devono essere tutti diversi tra loro
ovvero la successione o ordine degli elementi deve essere diversa
es: dato n= lama le permutazioni possono essere: laam, maal mala etc
sia ([ n ] ) il numero totale di elementi
e ( a ) quante volte l'elemento identico si ripete
La formula per calcolare questo numero di permutazioni e': P' (n/a) = n! / a!
PERMUTAZIONI CON RIPETIZIONE
PIU' ELEMENTI RIPETUTI PIU' VOLTE
ma essere tutti diversi tra loro
come mmaa, aamm, amam etc)
sia [ n ] il numero totale di elementi e [ a ] il numero di elementi uguali di un elemento [ b ] il numero di elementi uguali di un altro elemento [ c ] il numero di elementi uguali di un terzo elemento etc
La formula per calcolare questo numero di permutazioni e':
P'' (n / a,b,c,...w) = n! / a! * b! * c! * ... w!
ES: SCASSA = (6/2,3) = 6! / 2! 3!= 6 * 5 *4 * 3 *2 / 2 * 3 * 2 = 60
PERMUTAZIONI CIRCOLARI
Si applicano quando gli elementi di cui si vuole calcolare il numero di permutazioni
sono disposti in modo circolare. Come le ore di un orologio. Dati [ n ]elementi distinti, il numero delle permutazioni circolari [ P c ] è dato da Pc= (n-1)! Abbiamo visto che il numero di permutazioni semplici è dato da n! Perche' nelle permutazioni circolari non si considera un elemento? Dato che le permutazioni circolari si utilizzano quando gli elementi sono disposti in circolo,
e' evidente che non è possibile individuare sia il primo sia l'ultimo elemento. Ogni elemento puo' esserlo! Inoltre nelle permutazioni non ci devono essere nemmeno due sequenze uguali,
ma partendo via via dagli elementi in successione per formare i raggruppamenti
e mantenendo sempre un senso orario (indifferente se orario o antiorario)
si verificano delle sequenze identiche da scartare.
Si arriva a stabilire che queste permutazioni sono (n-1)!

1) dove gli elementi sono diversi tra loro (DISPOSIZIONI SEMPLICI]
2) dove gli elemeni possono ripetersi [DISPOSIZIONI CON RIPETIZIONE]
A differenza delle PERMUTAZIONI, la sequenza degli elementi (123) nell'insieme
e' indifferente, devono pero' differire di almeno un elemento:
321 312 213 231 132 123 Sono 6 insiemi distinti (caso 1)
233 333 113 321 111 112 Sono 6 insiemi distinti (caso 2) Gli elementi nell'insieme [ k ] possono essere: 1) TUTTI DIVERSI TRA LORO = disposizioni semplici con [ k < n ]
es: [ABCDEF] n=6 k=4
disposizioni= [ABCD] [DFAB] etc
-
2) POSSONO
RIPETERSI = disposizioni con ripetizione [ k < n oppure k > n ]
[ABCD] n=4 K=2 es: [AA] [AB] [CC] etc
[ABCD] n=4 K=6 es: [ABBCCA] [CABBDD] etc
DISPOSIZIONI SEMPLICI
Poiche' pero' come si vede nell'esempio sopra riportato
il denominatore e' inferiore al numeratore di tanti elementi fattoriali pari a[ k ] ,
e quindi semplificabile, si puo' direttamente passare alla formula:
D(n,k) = [n * (n-1) * ...] a scalare tante volte quanto vale [ k ] es: D(18,3) =scalare 3 volte da 18 = 18 * 17 * 16 D(20,5) = scalare 5 volte da 20 = 20*19*18*17*16
(PIU' ELEMENTI RIPETUTI PIU' VOLTE)
1) IN QUESTE DISPOSIZIONI [ k ] PUO' ESSERE [ > n ] oppure [ < n ]
(ma NON [ k = n ] perche' altrimenti sarebbe una PERMUTAZIONE)
2)UN ELEMENTO[ n ] PUO' ESSERE RIPETUTO SINO A[ k ] VOLTE
Formula: D' (n,k) = nk
es: QUANTE NUMERI DI 8 CIFRE SI POSSONO OTTENERE UTILIZZANDO LE CIFRE 0 E 1 ?

COMBINAZIONI SEMPLICI
gli n elementi sono tutti diversi tra loro e ogni k gruppo differisce dagli altri per almeno 1 elemento es: dati gli elementi 1;2;3 di classe 2
le combinazioni semplici possono essere solo 3: 12 13 32
la
formula

IL CALCOLO di C(3/2)
3! / 2! * (3-2)! = 3 *2 / 2 * 1 = 3
COMBINAZIONI CON RIPETIZIONE
nei gruppi lo stesso elemento puo' ripetersi sino a[ k ] volte ma non possono esserci gruppi con gli stessi elementi
A differenza delle combinazioni semplici, nel caso delle combinazioni con ripetizione non vi è alcuna limitazione su k, che
può essere un qualsiasi intero positivo anche maggiore di n.
ese: dati gli elementi 1;2 le combinazioni con ripetizione di classe3 possono esseresolo 4: 111 222 212 112
la formula:

IL CALCOLO di C'(2,3)
(2+3-1) ! / 3! * (2-1)! = 4! / 3* 1 = 4* 3 *2 / 3 *2 = 4
ATTENZIONE:
A volte si possono avere dubbi su quali sono gli elementi (n) e quale e' il gruppo (k)
Vediamo questo caso:
In quanti modi diversi posso distribuire 5 monete in 3 cassetti?
( ogni cassetto puo' contenere da 0 a 5 monete e le monete sono uguali)
A prima vista sembrerebbe che le monete siano gli oggetti(n) e i cassetti i contenitori o gruppi (k)
In realta' e' il contrario perche' l'insieme e' dato dal totale delle monete,
Immaginiamo di etichettare i cassetti con A B C e manteniamo fissa questa sequenza.
Se le monete fossero messe tutte nel primo cassetto avremo:
AAAAA se poi mettiamo 1 nel secondo avremo AAAAB 1 nel terzo AAABC etc
Ma se abbiamo BAAAA cosa vuol dire ? Abbiano invertito la sequenza dei cassetti e cio' non va bene!
Quindi AAAAB e AAABC AAABC e BAAAA Non possono essere una PERMUTAZIONE perche' nei diversi gruppi non ci sono sempre gli stessi elementi
Non possono' essere UNA DISPOSIZIONE perche' AAAAB e BAAAA alterano il significato QUINDI si tratta di una COMBINAZIONE con ripetizione n=3 e k=5
quindi (3+5-1) ! / 5! * (3-1)! = 7!/ / 5! * 2! = 7*6 *5*! /5! * 2 = 21

SCHEMA SU COME VALUTARE QUALE CALCOLO COMBINATORIO USARE

ESERCIZI
1) Siano date, in un'urna, 20 palline numerate (da 1 a 20).Senza tener conto dell'ordine, in quanti modi possibili diversi possono essere estratte 2 palline,
supponendo che, dopo ogni singola estrazione, la pallina venga
rimessa nell'urna? Si hanno dunque 20 oggetti che formano via via gruppi di 2 elementi.
n=20 ; k=2
Non e' una PERMUTAZIONE perche' n diverso da k
non e' una DISPOSIZIONE perche' i gruppi di 2 oggetti se riescono uguali non si contano
E' quindi una COMBINAZIONE ma con ripetizione dato che la pallina
estratta la prima volta puo' essere riestratta la seconda- percio' (n+k-1)! / k! (n-1)!
percio C'(20,2) = (20 +2 -1) ! / 2! * (20 -1 ) ! =210
Quanti sono gli anagrammi della parola MATEMATICA ? E una PERMUTAZIONE di n=10 di cui 3 A 2 T 2 M
10! / 3! * 2! * 2!
Una partita di calcio termina 4 a 4. In quanti modi teorici potrebbero essere stati via via segnati i goal delle 2 squadre? I gol sono in tutto 8 percio n=8 ma con 4 ripetizioni riconducibili alla sequenza base AAAABBBB
cioe' 2 elementi ripetuti 4 volte.
- Le sequenze possono essere diverse ? = SI
- Tutti gli elementi devono essere considerati ? SI
- Gli elementi si ripetono ? =SI
Si tratta di una PERMUTAZIONE con elementi ripetuti a=4 b=4 P''(8 / 4,4) = 8 ! / 4! * 4! = 8 * 7 * 6 * 5 * 4! / 4! * 4 * 3 * 2 = 7 * 6 *5 / 3 = 70 modi diversi
20 amici si rivedono e organizzano un incontro, ognuno stringe la mano a tutti gli altri.
Quante strette di mano ci saranno? - esiste un insieme di ragguppamento ? = SI - quanto vale ? =[ k ] =2 (ogni stretta di mano) - la sequenza o ordine e' importante ? = NO (la stretta tra 1 e 2 e' la stessa tra 2 e 1) -uno stesso elemento puo' essere ripetuto nell'insieme ? =NO (uno non stringe la mano a se stesso) percio' combinazioni semplici = C (10,2) = 20 ! / 2! * (20-2) !
8 persone si incontrano mensilmente sedendosi accanto lungo un tavolo.
Se ogni volta cambiano di posto, dopo quanti anni avranno esaurito
tutti i possibili abbinamenti? L'insieme k coincide con il numero degli elementi = SI = PERMUTAZIONE Ci sono elementi che si ripetono ? NO Permutazione semplice P(8,8) = 8! = 40320 Poiche' i mesi in un anno sono 12, sono necessari 40320 / 12 = 360 anni
Le targhe automobilistiche sono costituite da 2 lettere, seguite da 3 cifre,
seguite a loro volta da 2 lettere. Sapendo che le 2 lettere
possono essere scelte fra le 26 dell'alfabeto
calcolare quante automobili si possono immatricolare in questo modo ? La sequenza e' importante ? SI
gli elementi possono ripetersi ? SI = permutazioni con ripetizione
la risposta e' il prodotto di 3 calcoli
per le lettere si tratta di 2 insiemi di classe 2 utilizzando 26 elementi che possono ripetersi
Per i numeri di un gruppo k di 3 elementi che possono ripetersi scelti tra 10
D''(26,2) * D''(10,3) * D''(26,2) = 262 * 103 * 262 = 676 * 1000 *676
Nel sistema di numerazione decimale quanti numeri naturali di 4 cifre
contengono esattamente solo una volta ma contemporaneamente un 2, un 5 e un 8 (es 2685 oppure 1852 )
ma non con 0 in prima posizione ?
Se il numero fosse solo di 3 cifre si avrebbe la DISPOSIZIONE 3 ! = 6 possibilita'
Ma il gruppo e' di 4 cifre, che introduce il fatto che un altro numero
preso tra le altre 6 cifre restanti (1,3,4,6,7,9) (0 escluso come da richiesta) sia ad esempio in prima posizione.
I gruppi possibili diventano quindi 6 *6
Se invece il numero fosse in seconda posizione dovrei scegliee tra 7 numeri (0 compreso)
ed avrei in tutto 6*7 possibilita' di raggruppamento .
Questo caso e' identico a quelli con il numero da inserire in 3^ o 4^ posizione
Pertanto i casi possibili totali sono:
6*6 + 3 *( 6 * 7) = 162 numeri di 4 cifre che contengono contemporaneamente un 2 un 5 e un 8
Nel sistema di numerazione decimale quanti numeri naturali di 5 cifre
iniziano e finiscono con una cifra dispari?
Le cifre dispari sono in tutto 5 (1,3,5,7,9)
Il gruppo di 3 numeri interni sono formati dalle cifre da 0 a 9 che possono ripetersi
Pertanto si tratta di una DISPOSIZIONE CON RIPETIZIONE di 10 elementi di classe 3
D''(10,3) ovvero 103 = 1000
Le cifre dispari sono 5 ma messe all'inizio e alla fine e' come se
formassero dei numeri dispari di 2 cifre cioe' anche in questo caso
delle disposizioni con ripetizione di 5 elementi di classe 2 ovvero D''(5,2) = 52 =25
In tutto percio' 1000 *25 = 25000 possibilita'
John va 3 giorni alla settimana in palestra, dove ogni giorno pratica, uno sport diverso
scegliendo tra: pesi, nuoto, corsa. Fa percio' 3 sport alla settimana
. La palestra è aperta 7 giorni su 7
In quanti modi John può alternare i giorni di allenamento?
E se non vuole fare pesi il lunedi ? Per il primo quesito : Per prima cosa si deve scomporre la settimana in gruppi di 3 giorni: quanti gruppi si possono formare ? L'ordine e' importante ? NO perche' lunedi martedi venerdi e' la stessa cosa di martedi venerdi lunedi etc:
Quindi COMBINAZIONE SEMPLICE con n=7 k=3. C(7,3) = 7! / 3 ! * (7 – 3)! = 7 * 6 * 5 * 4! / 3 * 2 * 4! = 7 * 5 = 35 possibili combinazioni di 3 giorni in una settimana per ognumo di questi gruppi si praticano 3 sport diversi in possibili sequenza diverse
pesi, nuoto, corsa oppure nuoto, corsa, pesi etc
quindi si tratta di una permutazione di 3 elementi senza ripetizione P( 3) = 3! = 6 cioe' per ogni gruppo di 3 gg si possono alternare 6 attivita' dato che i gruppi sono 35 in tutto le possibilita' sono 35 * 6 = 210
Per il secondo quesito intuitivamente le possibilita' sono inferiori alle 210
cioe' si devono togliere dal totale dei casi in cui John non fara' pesi di lunedi, ma quanti sono ?
Si deve trovare quanti sono i casi in cui lo stesso sport cade nello stesso giorno della settimana.
Supponendo di fissare uno sport qualsiasi in un giorno della settimana vuol dire
che gli altri due sport sono praticati su 6 gg. Si tratta quindi di
trovare quanti gruppi di 2gg si formano con 6 gg cioe'
c(6,2) = 6!/2! * (6 – 2)! = 6 * 5 *4! / 2 * 4! = 6 *5 / 2 = 15 combinazioni di 2 giorni in questi 15 gruppi di due giorni si possono praticare alternativamente gli altri 2 sport cioe P(2) = 2! =2 In tutto le possibilita', escludendo il giorno fisso, sono 15 *2 =30 casi. Ora e' indifferente quale giorno sia stato stabilito per escludere uno sport qualsiasi. Dal totale dei casi si deve sottrarre il numero di casi in cui non
compare uno sport. In generale percio' 210-30=180. Che poi il giorno
sia lunedi e lo sport sia pesi e' indifferente, come e' lo stesso
risultato che si otterrebbe stabilendo che non si vuole fare corsa
il giovedi' oppure venerdi' etc.
Quante partite di dama diverse possono essere giocate da sei giocatori? L'ordine ha importanza ? no Gli elementi si ripetono ? No combinazioni semplici C(6,2) = 6! / 2! * (6-2)!= 6*5*4! / 2 * 4! = 3*5=15
Ad un torneo partecipano 10squadre.
Il torneo prevede 4 incontri tra ciascuna coppia di squdre:
2 partite in casa e 2 partite fuori casa (con la stessa squadra che
prima ha giocato in trasferta).
Quante partite verranno in tutto giocate?
D(10,2) = 10*9 = 90 incontri per una partita in casa e una fuori casa per 2 partite = 90 *2=180
Il numero di combinazioni di n elementi presi 4 a 4 e' uguale al numero di combinazioni presi 3 a 3.
Quanti sono gli elementi?
C(n/4) = C(n/3) ovvero
n!/4!*(n-4)! = n!/3!*(n-3)!
Semplificando i numeratori si ha: 4!(n-4)! = 3!(n-3)!
lo sviluppo di (n-3)! E' (n-3) (n-4)! e NON (n-3) (n-2)!
perche' la quantita' deve diminuire progressivamente di 1 quantita'
Da cui si ha: 4 *3!(n-4)! = 3! (n-3) (n-4)! e semplificando i due membri:
4 = n -3 da cui n=7
Nel totocalcio si deve indovinare l'esito di 14 partite utilizzando 1 X 2
in base al risultato. Quante schedine bisognerebbe giocare per avere la certezza di vincere?
La sequenza e' importante ? Si n=3
8 amici sono in una casa che ha 4 stanze ciascuna con 2 letti.
In quanti modi possibili possono stabilirsi? BR>
In generale quando vi sono piu' di 2 dati da considerare le possibilita' sono date dalla somma o prodotto dei singoli casi. In questo caso si devono calcolare i casi possibili per ogni stanza.
Per la prima stanza si deve vedere in quanti modi le 8 persone possono formare una coppia.
Ovviamente l'ordine non ha importanza e nemmeno si possono ripetere,
si tratta quindi di trovare la combinazione semplice di 8 elementi di k=2 percio'
C(8,2) = 8! / 2! * 6! = 4 * 7 = 28 per la seconda stanza ovviamente le persone da considerare non sono piu' otto
(perche' altrimenti la stessa coppia, gia' considerata, occuperebbe contemporaneamente due stanze)
percio si tratta di trovare C(6,2) e per la terza stanza C(4,2) e per la quarta C(2,2)
Il totale delle possibilita' e' quindi dato dal prototto delle singole combinazioni =
28 * 15 * 6 * 1 =1520
12 giocatori di tennis decidono di giocare un doppio
a) Quante coppie distinte si possono formare?
b) Una volta formate le coppie e mantendendo le coppie fisse, quante distinte partite (coppia contro coppia) si possono giocare?
risposta a: si tratta di una combinazione semplice di 12 elementi di classe 2.
C (12/2) = 12! / 2! *(12-2)! = 12*11*10! / 2! * 10! = 6*11=66 coppie
risposta b) si tratta di una combinazione semplice di 6 elementi di classe 2.
C (6/2) = 6! / 2! *(6-2)! = 6*5*4! / 2! * 4! = 3*5=15 partirte
Quanti numeri di 6 cifre tutte diverse tra loro posso ottenere stabilendo che
le prime tre cifre sono dispari e le ultime tre pari
In tutto le cifre pari, compreso lo 0, sono 5
i numeri di 3 cifre diverse vendo 5 elementi sono le D(5,3) = 5*4*3= 60
Lo stesso vale per le cifre dispari che solo D(5,3) =60
oertanto i numeri con le caratteristiche richieste sono 60 *60 = 3600
Uno studente deve dare in tutto 20 esami e ogni anno 5 esami diversi stabiliti per quell'anno accademico.
in quanti modi diversi puo' pianificare la sequenza degli esami ?
Per ogni anno puo' decidere la sequenza di 5 esami, cioe' una permutazione di 5 elementi ovvero 5 !
e questo per 4 anni.
In definitiva il suo piano puo' differenziarsi in 5! * 5! * 5! *5! modi diversi
Quante diagonali ha un poligono convesso di n lati ?
Si tratta di una caso combinatorio SENZA RIPETIZIONI
Innanzi tutto stabiliamo che la classe K e' =2 dato che una diagonale collega solo 2 elementi.
e gli elementi sono il numero dei vertici del poligono.
Combinatorio perche' una diagonale AB e' la stessa che BA (ovvero la sequenza deve essere diversa)
Senza ripetizioni perche' AA o BB non sono diagonali
Sul totale della combinazione si dovra' pero' intervenire dato che i lati non sono diagonali
Dunque: n sono i vertici del poligono ciascuno dei quali si collega ad un altro vertice (k=2)
Quindi ogni vertice si puo' collegare agli altri con la formula:
n! / k! * (n-k)!
Al risultato pero' dovra' essere sottratto il numero dei lati dato che questi non sono diagonali
Esempio: quante diagonali ha un esagono ?
n=6 k=2 6!/2*4! = 6*5*4*3*2 / 2*4*3*2 = 15 15-6 =9
Le diagonali di un esagono sono 9
19)
Calcolare il numero di modi distinti in cui puo' essere servito
un giocatore di scala quaranta in una singola mano .
Le carte sono n=108 per k=13
si tratta di combinazione senza ripetizione. C (108,13)
108! / 13 (108-13)!
20)
Lanciando una moneta 7 volte (e poi 7 volte etc),
in quanti casi diversi si ottiene 5 volte testa e 2 croce?
Si deve ragionare come se si trattasse di una parola formate da 7 lettere di cui 5 T e 2 C
Si tratta pertanto di una DISPOSIZIONE CON RIPETIZIONE si deve percio' applicare la formula:
n!/ 5! * 2! = 7!/5! * 2! = 7 *6 /2 = 21
Quindi come minimo si potranno fare 21 lanci (se si e' fortunati)
oppure tante volte finche' le 21 DISPOSIZIONI possibili non si siano realizzate
Partendo dalla casella 1 quanti percorsi possibili sono quelli per entrare nella casella 2
potendo fare solo traiettorie orizzontali e verticali?
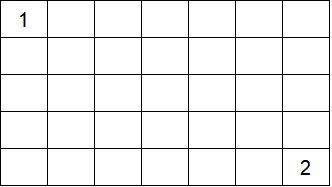
Qualunque percorso si faccia, si dovranno percorrere comunque 6 caselle orizzontali e 5 verticali
percio' in tutto 11 caselle, di cui 6 di un tipo e 5 dell'altro.
E' anche questo un caso di DISPOSIZIONE con RIPETIZIONE di 11 elementi di classe 6 e 5
Percio' 11! / 6! * 5! = 11!*10*9*8*7 = 462 PERCORSI
dati 3 numeri che possono assumere valori positivi interi quanti raggruppamenti possibili danno la somma 10?
poiche' pero' la somma 0+0+10 e' identica a 10+0+0 oppure 8+1+1=1+8+1
la loro sequenza e' indifferente percio' si tratta di una combinazione con ripetizione
n in questo caso sono i 3 numeri da considerare dell'insieme k =10 la formula delle COMBINAZIONI SENZA RIPETIZIONI e':
(n+k-1)!/k! * (n-1)!
da cui: (3+10-1)!/10! * 2!
12!/10!*7! = 12 *10*11* 10!/10! * 2! = 12*10*11/2 = 660
Se in una corsa partono 10 cavalli quante sono i possibili ordini di arrivo nelle prime 3 posizioni?
poiche' ai primi posti la sequenza di arrivo e' importante
la sequenza 123 e' da considerare diversa da 321
percio' NON e' una Permutazione perche' non tutti gli elementi sono coinvolti
NON e' una Combinazione perche' la sequenza e' importante
si tratta percio' di una Disposizione senza ripetizione (i 3 cavalli in arrivo sono diversi !)
quindi n=10 e k=3 PERMUTAZIONI SEMPLICI = n! / (n-k)! = 10! / 7! = 10*9*8 = 720 possibili ordini di arrivo
Usando le cifre 2,3,5,8,9 quanti numeri dispari di 4 cifre si possono avere?
Le permutazioni possibili sono n! = 5*4*3*2
i numeri dispari sono 3 su 5 ovvero i 3 /5 di n! cioe' 5*4*3*2 * 3 /5 = 72
Avendo 5 numeri di cui 2 pari e 3 dispari quanti sono i casi che i numeri dispari
occupino tutti e 3 una posizione dispari?
Poiche' i numeri possono cambiare di posizione, ma non ripetersi, si tratta
evidentemente di una DISPOSIZIONE sena ripetizione.
Ora se i numeri fossero solo 3 e tutti dispari, le disposizioni possibili sarebbero solo 3! = 6 --- esempio : 321, 231 132
Inserendo un solo numero pari all'interno in seconda posizione 3421 2431 1432 ect
o in quarta 3241 2341 1342 i 6 casi non aumenterebbero se la richiesta fosse di inserireR un solo numero pari all'interno
Se invece si introducessero due numeri pari nelle posizioni volute le possibilita' raddoppierebbero
es: 1 4 3 6 5 e 1 6 3 4 5
Quindi in totale le diposizione che rispondono al quesito sono 12.