Di seguito, lo spazio percorso viene considerato rettilineo.
Piu' il tempo, per percorrere uno spazio grande, e' piccolo piu' alta sara' la velocita' del corpo.
La velocita' pertanto si misura in metri al secondo m/s
se espressa in kilometri all'ora (km/h) occorre moltiplicare il valore della velocita' dei m/s per 3,6
(dato che in 1 chilometro ci sono 1000 metri e in ora 3600 secondi)
e viceversa per passare dai km/h ai m/s occorre dividere il valore della velocita' per 3,6
In generale abbiamo v = s / t o meglio v=Δs / Δt
dove Δs= s-s0 ovvero la distanza tra punto fnale e punto iniziale e Δt= t-t0 ovvero la differenza di tempo tra la fine e l'inizio del moto
Occorre pero' distinguere la velocita' media (espressa come ṽ) dalla velocita' istantanea ovvero un corpo puo' variare nel tempo la sua velocita'.
Ad esempio se un corpo percorre 20 m in 2 secondi la sua velocita' media e' di 10 m/s
ma in 4 istanti la velocita' istantanea poteva essere di: 28 m/s di 2m/s , 6m/s e 4 m/s
la formula che esprime la velocita' media e:
[1] ṽ = s-s0 / t-t0
il grafico (fig.1) che descrive la velocita' media e':
figura 1
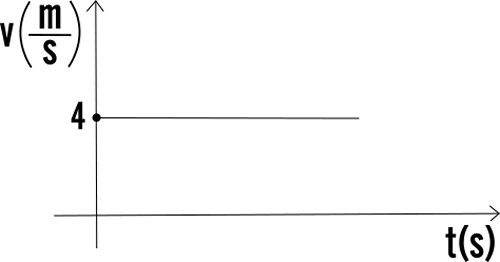
figura 2
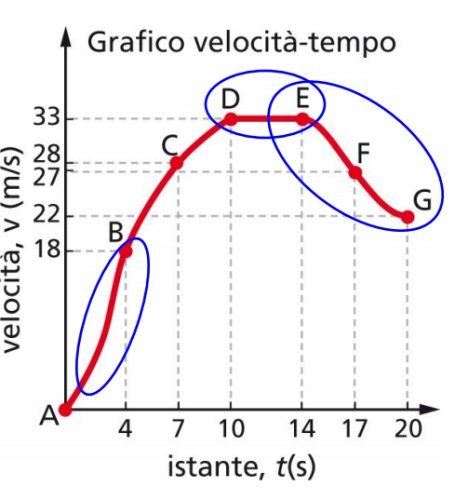
Osservando il grafico di fig.1 si può affermare che, essendo lo spazio percorso uguale a s= v * t
questo corrisponde esattamente all'area di un rettangolo (fig. 3) individuato nell'istante t alla velocita' v
fig.3

Se l'istante t0 e' 0 si ha: ṽ = s-s0 / t
da cui lo spazio percorso e' dato [2] s = s0 + ṽ * t
La
variazione di velocita' e' detta accelerazione, ovvero come varia la
velocita' nel tempo.
Anche
per l'accelerazione si puo' avere una accelerazione media indicata
con ā o una accelerazione istantanea (a).
Occupandoci
del
MOTO
RETTILINEO UNIFORMEMENTE ACCELERATO (MRUA)
ovvero
con accelerazione costante (che non varia) l'accelerazione media
coincide con l'accelerazione:
ā=a
a=
ā= Δv / Δt
in
questo tipo di moto la velocita' aumenta progressivamente in modo
costante.
Ovvero, la velocita' di un corpo, ad ogni secondo, aumenta' di una "quantita' pari all'accelerazione.
Percio' se un corpo parte da fermo con accelerazione uniforme di 10 m/s, dopo 10'' la sua velocita' sara' di 100 m/s.
Infatti
essendo
Δv = a * Δt
si evidenzia che la velocita' e' direttamente proporzionale al tempo del
moto.
La
relazione tra velocita' e tempo, e' espresa da un grafico in cui l'inclinazione della retta
dipende dalla grandezza della accelerazione.
Quanto piu' l'accelerazione e' alta, piu' la retta tende alla verticalizzazione.
Nel grafico di fig.4 si nota che nell'istante zero il corpo possiede gia' una velocita' iniziale.
figura 4
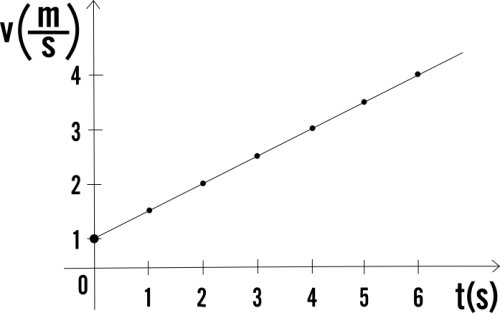
Se
consideriamo un corpo gia' in movimento con velocita' inziale v0
a partire dal tempo
t0
avremo che la relazione
con al velocita' finale v
sara':
v
- v0
= a * (t - t0
)
se
il tempo iniziale
t0
e' uguale a 0 abbiamo la relazione
[3]
v = v0
+
a * t
DETTA LEGGE DELLA VELOCITA'
Se
v0
fosse uguale a zero, cioe' il corpo partisse da fermo avremo semplicemente:
v = a * t
da cui
[3.1] a= v / t
L'accelerazione si misura pertanto in metri al secondo al quadrato.
Infatti se nella [3.1] si precisassero le unita' di misura , poiche'
v= m/s
si avrebbe
a= (m /s ) /s
a= m /s2
Ma cosa significa secondi al quadrato ?
Questa e' solo una rappresentazone sintetica del concetto che un corpo aumenta la sua velocita' (che e' in m/s) ad ogni secondo
In pratica questo significa che se un corpo ha una accelerazione costante di 3 m/s
dopo 1 secondo la sua velocita' sara' di 6 m/s e dopo un altro secondo la sua velocita' aumenta a 9 m/s etc
Sarebbe piu' corretta (logicamente) questa simbologia m/s * (s)
Vediamo
ora la relazione tra accelerazione e spazio.
Come
detto nell'accelerazione le velocita' variano
ma la velocita'
media ṽ in un moto accelerato e' data tra la media
della velocita' inizale v0
e quella finale v
ovvero
[4
] ṽ = ( v0 + v ) / 2
In un MRUA lo spazio A-B percorso nell'intervallo di tempo puo' essere calcolato utilizzando
le velocita' media tra A e B ovvero [V(A)+V(A)]/ 2
riprendendo
la formula [2] del moto rettilinneo uniforme
s = s0 +
ṽ * t
e
sostituendo in essa la ṽ media nel MRUA ovvero la
[4] - abbiamo
[5]
s = s0 + { ( v0
+ v ) * t } / 2
sostituendo
nella [5] il valore v della
[3] si ottiene
s
= s0 + { ( v0 +
v0
+ a * t ) *t} /2
e
procedendo algebricamente otteniamo
s
= s0 + { ( 2v0 *
t + a * t 2 } /2
[
6 ] s = s0 + v0
* t + ( a * t 2 }
/2 che e' la legge oraria
del MRUA
se nella [6] si considera velocita' iniziale e punto iniziale uguali a zero
si
ottiene ch lo spazio percorso
[7]
s = a * t 2 /
2
la
[7] e' simile ad una equazione tipo Y = a X2
ovvero di una parabola
considerando un corpo che cade da una altezza qualsiasi con
accelerazione di gravita' pari a 9,8 m/s il grafico (fig.5) mostra la relazione spazio tempo
e le corrispondenti velocita' espresse sia in m/s (=Km/h /3,6) sia in km /h (=m/s * 3,6)
figura 5

Trasformando
e sostituendo nelle varie formule si puo' ricavare che
Δs=
(v2 – v0 2
) / 2 * a
e
l'inversa
a=
(v2 – v0 2
) / 2 * Δs
Ragionamdo sul diagramma di fig. 5, essendo la curva, come detto, una parabola,
il coefficiente angolare di una retta tangente un punto qualsiasi della curva, sarebbe
la velocita' istantanea in quell'istante. (vedere esempio 3)
****** ESERCIZI *******
1)
Un corpo parte da fermo e dopo 25 secondi raggiunge la velocita' di 80 m/s. Quanto spazio ha percorso ?
Attenzione a non confondere la s del tempo espresso in secondi e la s riferita allo spazio
Si tratta di un moto accelerato con t(0)=0 e s(0)=0
per conoscere lo spazio s si deve calcolare la sua accelerazione
pertanto a= v / t a= 80 m/s / 25 s = 3,2 m/s 2
e lo spazio percorso sara'
s= 1 / 2 * 3,2 m/s2 * ( 25 m/s )2 = 1000 m
2)Esercizio tratto da Tutorial di fisica - Arrigo Amadori
Consideriamo due automobili: A1 davanti e A2 dietro.
Entrambe si muovono con velocità costante pari a
108 km/h (30 m/s)
lungo una strada rettilinea e che le due auto siano alla distanza di
20 m l'una dall'altra
Ad un certo istante, t=0, la macchina (A1)
improvvisamente inizia a frenare.
in modo
costante,quindi con accelerazione negativa costante,
e che la frenata duri 5''
prima che l'auto sia
completamente ferma.
L'auto A2 che segue inizia a frenare dopo
un tempo di reazione di
1''
Supponiamo anche che il "modo" di frenare dell'auto
A2 sia lo stesso di quello dell'auto
A1 .
Prendiamo l'origine dello spazio ( s = 0 ) coincidente con il
davanti dell'auto A2 all'istante iniziale t = 0 .
In questo modo abbiamo completato la definizione del sistema di riferimento.
Cosa succederà ? L'auto A2 tamponerà A1 ?
All'istante iniziale t = 0 la situazione delle due auto è quindi la
seguente :

Consideriamo ora il moto dell'auto A1 e deduciamone
l'equazione spazio-tempo del moto.
Supponendo la frenata uniforme, ricaviamo l'accelerazione (negativa)
corrispondente :
![]() .
.
Il moto di A1 è un moto rettilineo uniformemente accelerato per cui
la sua equazione spazio-tempo
sarà :
![]() .
.
Nel nostro caso, essendo lo spazio iniziale di A1 pari a 20 m
e la velocità iniziale 30 m/s , si avrà :
![]()
da cui, semplificando :
![]() .
.
Consideriamo ora il moto agli istanti t = 0, 1, 2, 3, 4, 5, 6 . Otteniamo
perciò, facendo i calcoli, la
seguente tabella oraria :

si noti che dopo t = 5 l'auto A1 , avendo completamente
frenato, rimane ferma,
per cui la sua
posizione 95 metri dopo l'inizio della frenate non cambia.
Consideriamo ora il moto dell'auto A2 limitandoci per
semplicità a considerare che esso è un moto
rettilineo uniforme da t = 0 a t = 1 ( 1 secondo
è il tempo di reazione di A2 ) mentre diventa
uniformemente accelerato in seguito allo stesso modo di A1 ,
perché si presuppone che le due auto
abbiano un identico sistema di frenata.
Otterremo allora la seguente tabella oraria :

(l'abbiamo ottenuta semplicemente aggiungendo a 30 (la posizione
all'istante t = 1 ) la differenza
di spazio fra 47 - 20 della precedente tabella ecc.)
Riportiamo ora questi dati su un diagramma spazio-tempo e disegniamo i grafici
del moto delle due
auto :

Dal grafico si vede bene che un po' prima dell'istante t = 4 l'auto
A2 tamponerà l'auto A1 !!!
3) Esercizio
Verifichiamo che il coefficiente angolare (m) della retta tangente alla parabola di fig.5 a 10''
e' proprio quello riportato nella tabella a fianco cioe'=98 che esprime la velocita' in quell'istante.
L'equazione generica della parabola e':
y = 1/2 * m * x^2
che coincide con la formula della relazione della accelerazione spazio/tempo ovvero
s= 1/2 * a * t^2
sostituendo i valori abbiamo:
s= 1/2 * 9,8 * 10^2 = 490
ma lo spazio e' rappresentato sull'asse delle y percio' si ha che s=y=490
Ora occorre trovare il coefficiente angolare ( m )della tangente nel punto di coordinate 10,490
L'equazione generica di una retta passante per i punti noti x0 e yo e':
y - y0 = m * (x - x0)
sostituendo i valori otteniamo:
y - 490 = m ( x - 10)
da cui si ricava che
y = mx - 10m +490
ora, poiche' questa retta deve essere tangente alla parabola
si devono mettere in relazione (in sistema) le rispettive equazioni
y = mx - 10m +490 (retta)
y = 1/2 * 9,8 * x^2 (parabola)
da cui si ottiene per sostituzione :
1/2 * 9,8 * x^2 = mx -10m +490
e ordinando rispetto alle x otteniamo:
4,9 * x^2 - mx + 10m -490 = 0 [eq. 1]
che ' una equazione di secondo grado
che si risolve con la formula classica :
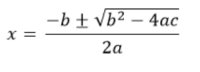
La condizione di tangenza e' che il discriminante o delta (b^2 - 4ac) della equazione sia uguale a zero
cioe' ammetta un'unica soluzione rispetto alle x
(covvero un solo valore di x, perche' se fossero 2 la retta sarebbe secante alla parabola incontrandola in 2 punti)
quindi per l'[eq.1]
si ha che b^2=m^2 e 4ac= 4*4,9*(10m-490)
e porre la condizione uguale a zero
m^2 -4*4,9* (10m -490)=0
questa diventa a sua volta una equazione di secondo grado rispetto ad (m) che e' il valore che dobbiamo trovare
m^2 - 19,6 * 10m - 19,6*490 =0
per trovare m applichiamo la solita formula dove
b^2 = 196 *196 = 38416
-4ac=-4*19,6*490 = 38416
il che porta da azzerare il discriminante, restando solo
m= -b / 2a
m= -(-196) / 2
m=98
che' esattamente il valore della velocita' dopo 10'' (come da tabella e da calcolo)